Multithreading in C++. Part 1.
Starting with the C++11 standard, C++ provides support for writing portable multitheaded applications without relying on additional libraries and extensions. The basic functions and classes for thread support are declared in the <thread> header. Check the definition here.
We introduce threads with the ubiquitous hello thread program.
Creating threads
Starting a new thead in C++ is done by constructing a new std::thread object. Thread execution begins immediately after the thread object is constructed. A simple example,
#include <iostream>
#include <thread>
// every thread has an "entry" function
void hello() {
std::cout << "hello thread\n";
}
int main()
{
std::thread t(hello);
t.join();
return 0;
}
Thread execution starts at the entry or top level function passed as an argument to the thread object constructor. In the example above the entry or top level function is hello().
Since the return value of the top level function is ignored, it usually returns void.
Note that the program now has two threads, the initial one running main() and the one we have created. The call to join() is important, otherwise the main thread could finish before the thread t.
Note that we can choose detach() instead of join(). In this case the thread would continue even after the main thread finished. In either case, we need to choose one of the two options, otherwise when the thread destructor is called it terminates our program. Almost in all use cases we use join().
Function Objects and Lambdas
In addition to functions, threads can be passed function objects or lambdas as parameters. For example
#include <iostream>
#include <thread>
struct bg_task{
void operator() (){
std::cout<<"function object \n";
}
};
int main(){
std::thread a(bg_task{});
std::thread b([](){
std::cout<<"calling lambda\n";
});
a.join();
b.join();
}
You can try this simple example here. Note that when using gcc we need to pass the pthread switch.
So far we have used std::thread::join which we use almost exclusively. The example below is an illustration of the use of detach.
#include <iostream>
#include <thread>
#include <fstream>
#define WAIT
void write_to_file() {
std::ofstream output;
output.open("output.txt");
output << "first line\n";
output << "second line\n";
output.close();
}
int main()
{
std::thread t{ write_to_file };
t.detach();
#ifdef WAIT
std::this_thread::sleep_for(std::chrono::minutes(1));
#endif
}
As you can see we use detach() instead of join(). Therefore the calling thread (in this case main) does not wait for the thread t. But when the main thread exists all other threads are destroyed. Therefore the created thread might not have enough time to perform its job. You can see these two cases by defining and undefining WAIT in the code.
In class exercise 0
Write two function, each running in its own thead. The first read_input keeps reading input from std::cin until the user types “quit”. The second one,read_file reads the content of (a one line) file. To simulate a time consuming I/O operations the read_file function should sleep for 10 seconds.
Create a text file in the same directory as your VC++ solution, call it “input.txt” and write a one liner in it.
#include <iostream>
#include <fstream>
#include <thread>
#include <chrono>
void read_input() {
std::string s;
std::cout << "enter a string. Type 'quit' to quit\n";
while (s != "quit") {
std::cin >> s;
std::cout << "user input= " << s << "\n";
}
}
void read_file(std::string name) {
std::ifstream file;
std::string content;
std::this_thread::sleep_for(std::chrono::seconds(10));
file.open(name);
std::getline(file, content);
std::cout << "content of file =" << content << "\n";
file.close();
}
int main()
{
std::thread t(read_file,"input.txt");
std::thread t2(read_input);
t.join();
t2.join();
std::cout << "main thread done\n";
}
Handling exceptions
We close this section by considering the case when an exception is thrown before a thread is joined. Consider the following code
#include <iostream>
#include <thread>
#include <exception>
void myf(){
throw std::exception{};
}
void runt(){
std::thread t([](){std::cout<<"started thread\n";});
myf();
t.join();
}
int main(){
try {
runt();
}
catch(std::exception e){
std::cout<<e.what()<<"\n";
}
std::cout<<"main thread is done\n";
}
Try running this code here.
As you can see the statement std::cout<<"main thread is done\n" is never reached. This is because when the destructor of a thread object is called (i.e. ~std::thread()) it calls std::terminate() if the thread is joinable. Calling std::thread::join() or std::thread::detach() make the thread not joinable and therefore does not call std::terminate().
In the above example, t.join() is never reached because myf() throws an exception. Therefore t.~thread() calls std::terminate().
One way to guard against such a situation to use the Resource acquisition is initialization (RAII) technique. We will see more of this technique when we study mutexes and locks but for now it is sufficient to say that we construct an object wrapper around the thread so that it automatically calls join() when it is destroyed.
In the code below we define a class thread_guard that automatically calls join when its destructor is called. Since the destructor is called when the object goes out of scope this guarantees that the created thread will be joined even when the scope that created the thread takes an unexpected flow due to exceptions.
#include <iostream>
#include <exception>
#include <thread>
void threadf() {}
void throwf() {
std::cout << "starting throwf\n";
throw std::exception{ };
}
struct thread_guard {
std::thread& _t;
thread_guard(std::thread& t) :_t(t) { }
~thread_guard() {
if(_t.joinable())
_t.join();
std::cout << "thread guard dtor\n";
}
};
void runt() {
std::thread t(threadf);
thread_guard g(t);
throwf();
}
int main()
{
try {
runt();
}
catch (std::exception & e) {
std::cout<<e.what()<<"\n";
}
std::cout << "main thread is done\n";
}
You can try the above code here
Our solution does not guard against the case when an exception occurs inside the thread code. In the previous example if the thread t runs function throwf instead of threadf our thread_guard solution does not work. This is because exceptions are not transferred between threads so we need to handle it locally. One solution is to provide an exception safe wrapper as in the example below.
#include <iostream>
#include <exception>
#include <thread>
void threadf() {}
void throwf() {
std::cout << "starting throwf\n";
throw std::exception{ };
}
struct thread_guard {
std::thread& _t;
thread_guard(std::thread& t) :_t(t) { }
~thread_guard() {
if(_t.joinable())
_t.join();
std::cout << "thread guard dtor\n";
}
};
void runt() {
std::thread t(throwf);
thread_guard g(t);
throwf();
}
template<typename F>
void wrapper(F f){
try{
f();
}
catch(...){}
}
int main()
{
std::thread t(wrapper<void (*)()>,throwf);
t.join();
std::cout << "main thread is done\n";
}
You can try the code here.
In this case the compiler can not automatically deduce the template parameter type F because we are calling wrapper indirectly inside a thread object. Compare that with just calling from main wrapper(throwf) which the compiler can automatically deduce.
If passing the type of throwf to the template looks complicated you can use decltype, i.e.
std::thread t(wrapper<decltype(throwf)>,throwf)
Passing parameters
Passing arguments to the function is done by passing extra arguments to the thread constructor. For example,
#include <iostream>
#include <thread>
struct fobj{
void operator()(std::string s){
std::cout<<s<<"\n";
}
};
void threadf(std::string s){
std::cout<<s<<std::endl;
}
int main(){
int x=0;
std::thread q(fobj{},"Hello function object");
std::thread p([](std::string s){
std::cout<<s<<"\n";
},"Hello lambda");
std::thread t(threadf,"hello function");
p.join();
q.join();
t.join();
}
You can try the above code here.
Internally, the thread constructor passes arguments to the callable object as an rvalue.
Therefore if the callable object expects the argument to be a reference then use std::ref.
The code below will not compile
#include <iostream>
#include <thread>
void threadf(int& x){
x=17;
}
int main(){
int x=2;
std::thread t(threadf,x);
t.join();
std::cout<<x<<std::endl;
}
But this one does, note the use of std::ref.
#include <iostream>
#include <thread>
void threadf(int& x){
x=17;
}
int main(){
int x=2;
std::thread t(threadf,std::ref(x));
t.join();
std::cout<<x<<std::endl;
}
Try it here.
The situation is similar to the following example:
void func(int &x){
}
template<typename T,typename U>
void g(T f,U&& x){
f(std::move(x));
}
int main(){
int x=17;
g(func,x);
}
You can try it here.
A different way of passing parameters by reference would be to use a function object that stores a reference to the variable. Example
#include <thread>
#include <iostream>
struct foo {
int& _x;
foo(int& x) :_x(x) {}
void operator()() {
_x = 19;
}
};
int main(){
int x=8;
std::thread t(foo{x});
t.join();
std::cout<<x<<"\n";
}
In class exercise 1
In this exercise we use two threads to generate two large random prime numbers. We compare the performance with a sequential version where the generator is called twice in a row.
First we write the random number generator and the selection of primes
#include <iostream>
#include <thread>
#include <random>
/* a simple function to sample large random numbers */
std::random_device rd;
const int lowest=4000000;
const int highest=8000000;
std::uniform_int_distribution<int> dist(lowest, highest);
inline int get_rand() {
return dist(rd);
}
bool is_prime(int value) {
/* this is NOT the most efficient way of
* determining if a number is prime */
if (value <= 1)return true;
for (int i = 2; i < value; ++i)
if (value % i == 0) return false;
return true;
}
The above allows us to generate a random number between lowest and highest then test if it is a prime number. Note that is_prime() is not the most efficient way of testing a prime. In any case we prefer this so that each thread has sufficiently large computations to perform.
To have enough probability to select a prime we repeat the above n times until we find a prime number as shown below.
/* A function that samples random numbers until it finds a prime.
* Gives up and returns 0 after n tries
*/
int get_large_prime(int n) {
int large;
for (int i = 0; i < n; ++i) {
large = get_rand();
if (is_prime(large))return large;
}
return 0;
}
We call the above code twice, sequentially, and measure the duration.
int main(){
const int num_tries = 300;
auto start = std::chrono::high_resolution_clock::now();
int v1,v2;
std::cout << "starting sequential\n";
v1=get_large_prime(num_tries);
v2 = get_large_prime(num_tries);
auto end = std::chrono::high_resolution_clock::now();
auto duration = std::chrono::duration<double, std::ratio<1, 1000>>(end - start);
std::cout << "values found " << v1 << " and " << v2 << std::endl;
std::cout << "sequential time = " << duration.count() << std::endl;
}
On an i7 this takes about 26 milliseconds.
To perform the two operations in parallel, since we have multiple cores, we run get_large_prime in two separate threads. Since a std::thread object ignores the return value of the top level function we must pass a variable by reference to retrieve the prime number. Therefore we overload get_large_prime as follows:
/* to be used with threads */
void get_large_prime(int n,int& result) {
int large;
result=0;
for (int i = 0; i < n; ++i) {
large = get_rand();
if (is_prime(large)){
result=large;
return ;
}
}
return ;
}
And the main function
int main(){
const int num_tries = 300;
auto start = std::chrono::high_resolution_clock::now();
int v1,v2;
std::cout << " starting two threads \n";
auto start = std::chrono::high_resolution_clock::now();
/* start two threads here and call the
* the function you wrote to get a large prime
*/
std::thread t1(get_large_prime,num_tries, std::ref(v1));
std::thread t2(get_large_prime,num_tries, std::ref(v2));
t1.join(); t2.join();
auto end = std::chrono::high_resolution_clock::now();
auto duration = std::chrono::duration<double, std::ratio<1, 1000>>(end - start);
std::cout << "values found " << v1 << " and " << v2 << std::endl;
std::cout << "two threads time = " << duration.count() << std::endl;
}
Unfortunately, with threads the compiler doesn’t know which version to use. You can try the above [here] (https://godbolt.org/z/jWhjqK) to see the error.
The simplest solution is to give a different name for the two versions. A different way is to help the compiler which allows us to use the same name.
...
using FType = void (*)(int, int&);
FType f = get_large_prime;
std::thread t1(f,num_tries, std::ref(v1));
std::thread t2(f),num_tries, std::ref(v2));
...
You can try this solution here.
Transferring thread ownership
Sometimes we need to transfer ownership of thread. For example, we we need to store threads in containers. But thread objects are not copyable. Only one thread object can be associated with a thread of execution at any given time. In these cases we must use move semantics.
Here an example to illustrate the problem. For simplicity we define a Container class that holds a single item. Typically, a container would add a copy of an object of arbitrary type which does not work with threads.
#include <iostream>
#include <thread>
void threadf() {}
template<typename T>
struct Container {
T _t;
Container() {
std::cout << "general\n";
}
void addItem(const T& t) {
_t = t;
}
T& getItem() {
return _t;
}
};
struct Tclass{
};
int main() {
std::thread t(threadf);
Tclass obj;
Container<std::thread> tc;
Container<Tclass> oc;
tc.addItem(t);
oc.addItem(obj);
tc.getItem().join();
std::cout << "main thread is done\n";
}
If you run the above code here the compiler will give an error similar to “use of deleted function operator=” because it is deleted for std::tread objects.
One solution would be to specialize the template for Container, i.e. add the following code
template<>
struct Container<std::thread> {
std::thread _t;
Container() {
std::cout << "specialized\n";
}
void addItem(std::thread& t) {
_t = std::move(t);
}
std::thread & getItem() {
return _t;
}
};
As you can see the addItem method uses std::move when T=std::thread.
A better method which is used by STL containers is to have two versions of addItem: one that takes a constant reference and the other an rvalue reference as show in the code below.
#include <iostream>
#include <thread>
void threadf() {
}
template<typename T>
struct Container {
T _t;
void addItem(T& t) {
_t = t;
}
void addItem(T&& t) {
_t = std::move(t);
}
T& getItem() {
return _t;
}
};
struct Tclass{
};
int main() {
std::thread t(threadf);
Tclass obj;
Container<std::thread> tc;
Container<Tclass> oc;
tc.addItem(std::move(t));
oc.addItem(obj);
tc.getItem().join();
std::cout << "main thread is done\n";
}
You can test the code here
In class exercise 2 (Note on compiler optimization)
In many of the examples we compare the performance of single vs multi threaded versions. Since our focus is on performance we don’t use the result of the single threaded version unless we need to check the correctness of the multi-threaded version.
This approach sometimes leads to surprising results because of compiler optimizations. In particular, dead code elimination. The basic idea is that if a variable or the output of a function is not used, the compiler might not include the function in the executable. In that case the duration of the function call is (close to) zero.
Let us illustrate with an example of sequential code.
#include <iostream>
#include <vector>
#include <random>
#include <algorithm>
#include <chrono>
int main(){
std::random_device rd;
std::uniform_int_distribution<int> dist(1,1000);
const int n=5000000;
std::vector<int> v(n);
std::generate(v.begin(),v.end(),[&](){return dist(rd);});
auto start=std::chrono::high_resolution_clock::now();
bool result=std::any_of(v.begin(),v.end(),
[](int x){return x==2000;}
);
auto end=std::chrono::high_resolution_clock::now();
auto duration=
std::chrono::duration<double,std::milli>(end-start);
std::cout<<"duration = "<<duration.count()<<"\n";
std::cout<<"value found ="<<std::boolalpha<<result<<"\n";
}
You can try the above code here
The duration is either close to zero or about 2.3 milliseconds depending on if
we remove the last line that prints the value of result or not.
The reason is that when we don’t print (i.e. not use) the variable result the compiler removes it from the code. This can be seen below in the assembly output between the two calls to now().



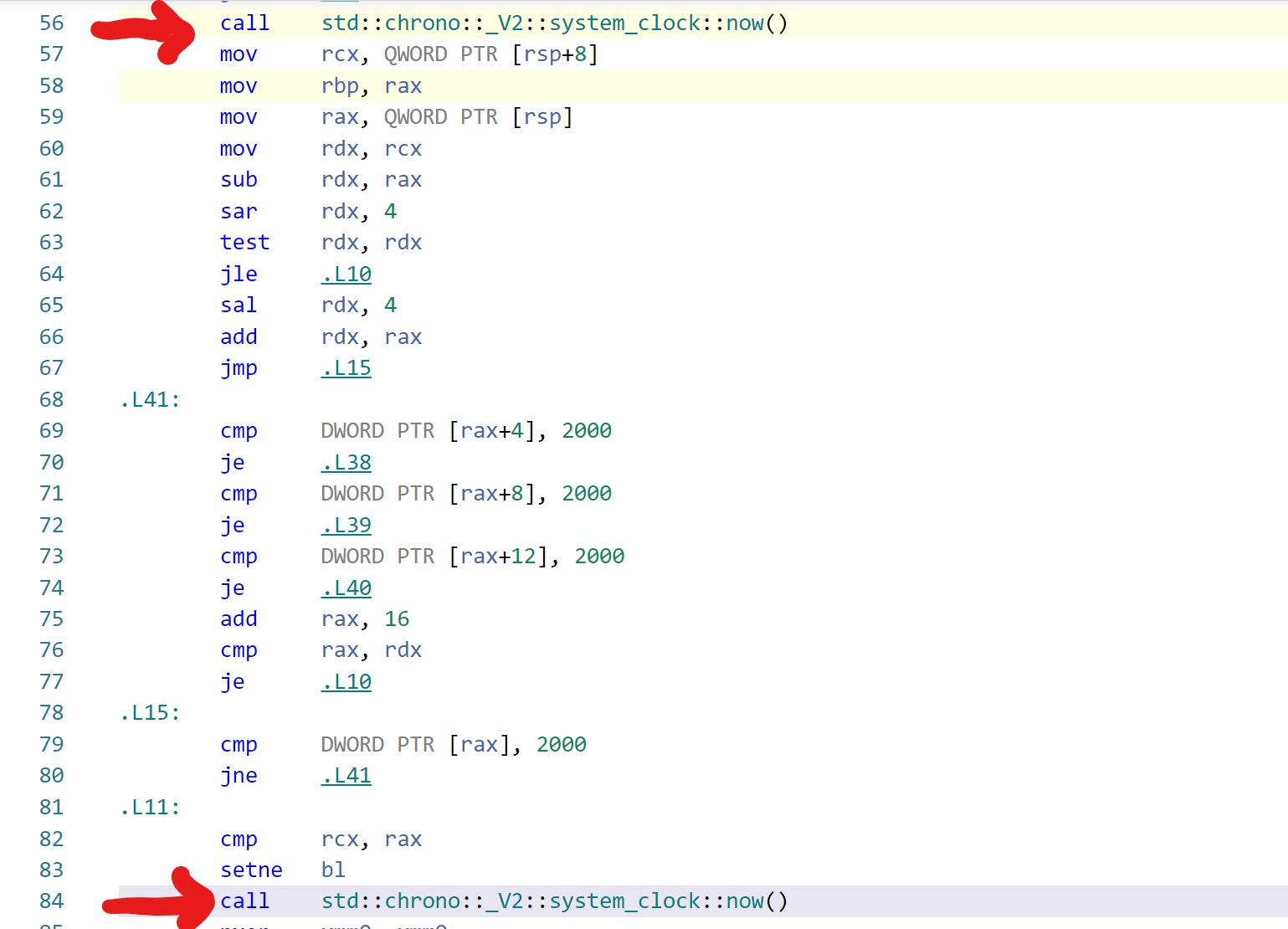
Figure 1 shows the assembly output when the last line is not included. Note the absence of instructions between the two calls to now().
Figure 2 shows the assembly output when the last line is included. Note the number of instructions between the two calls to now().
In class exercise 3
In this exercise we will build a multi-threaded program to determine if a large vector of integers contains a certain value.
This is the parallel version of STL std::any_of( we will see later that STL algorithms can also be parallelized easily)
The basic idea is to divide the range into as many blocks as there are hardware threads. For each block, a thread, independently, searches that block for the value.
When all the threads are done, if any of them as found a value in its own block we conclude that the vector contains that value.
To collect the results of threads we define std::vector<bool> results(num_threads). thread i, will store its result in results[i].
The function contains takes a starting and ending iterators denoting a particular block of the vector. The reason we use a bool iterator for the results instead of, say, passing result[i] by reference is that the implementation of std::vector<bool> is a specialization of std::vector. In particular operator[] returns a value not a reference like the general implementation.
In the example below we search for a non-existent value to maximize the running time.
/* Given a vector v of n integers:
* Write a function to test if v
* contains a certain number at least once.
* Use as many threads as your hardware permits.
*/
#include <iostream>
#include <thread>
#include <vector>
#include <chrono>
#include <random>
#include <algorithm>
template<typename T>
void print_duration(T start, T end,std::string s) {
auto duration = std::chrono::duration<double, std::ratio<1, 1000>>(end - start);
std::cout << "\nduration "<<s <<" "<< duration.count() << "\n";
}
/* note that the range is
* a semi closed interval [first,last)
*/
template<typename Iter,typename T,typename IterBool>
void contains(Iter first, Iter last, T value,IterBool result);
/* see the lecture notes for the reason we use
* an iterator for the bool instead of passing a bool
* variable by reference
*/
template<typename Iter,typename T,typename IterBool>
void contains(Iter first, Iter last, T value,IterBool result) {
Iter itr = first;
*result = false;
while (itr != last) {
if (*itr == value) {
*result = true;
return;
}
++itr;
}
return ;
}
int main()
{
/* choose size power of two */
const int n = 2 << 25;
std::random_device rd;
std::uniform_int_distribution<int> dist(1, 10000);
/* choosing a value that is NOT in the vector*/
int value = 12000;
std::vector<int> v(n);
std::generate(v.begin(), v.end(), [&]() {return dist(rd); });
using Iter = std::vector<int>::iterator;
/* using the sequential STL std::any_of() */
auto start = std::chrono::high_resolution_clock::now();
bool res = std::any_of(v.begin(), v.end(), [=](int x) {return x == value; });
std::cout << "sequential result = " << std::boolalpha << res << std::endl;
auto end = std::chrono::high_resolution_clock::now();
print_duration(start, end, "sequential ");
/* Using our implementation with the number of
* threads equal to the hardware threads
*/
int num_threads = std::thread::hardware_concurrency();
int block_size = n / num_threads;
/* store the result of each block in vector results */
std::vector<bool> results(num_threads);
std::vector<std::thread> mythreads;
Iter begin = v.begin();
auto itr = results.begin();
start = std::chrono::high_resolution_clock::now();
/* declaring i as long long to avoid warning
* when we use it for iterator arithmetics
* since iterators on x64 are 8 bytes
*/
/* divide the input into blocks equal to the
* number of threads
*/
for (long long i = 0; i < num_threads; ++i) {
/* we can do such arithmetic because
* vector iterators are random iterators
*/
Iter first = begin + i * block_size;
Iter last = begin + (i + 1) * block_size;
mythreads.push_back(
std::thread(
contains<Iter, int, decltype(itr)>, first, last, value, itr)
);
++itr;
}
for (auto& t : mythreads)
t.join();
end = std::chrono::high_resolution_clock::now();
print_duration(start, end, "multiple threads");
constexpr auto identity = [](auto r) {return r; };
/* combine the results of blocks */
std::cout<<"multiple thread result "<<
std::any_of(results.begin(), results.end(),
identity)<< "\n";
}
Example: parallel accumulate
In its simplest form, std::accumulate adds( accumulates) all the values in a given range,
including a supplied initial value. The default operation is std::plus{}, the first
call to std::accumulate below can be written as
std::accumulate(v.begin(),v.end(),0,std::plus{}). We can supply any binary operator,
for example, in the second call below, we use std::multiplies.
NOTE: if you are using a pre c++17 compiler you might need to supply template parameter
for std::multiplies{}, e.g. std::multiplies<int>{}.
#include <iostream>
#include <numeric>
#include <functional>
#include <vector>
int main(){
std::vector<int> v{1,2,3,4};
std::cout<<
std::accumulate(v.begin(),v.end(),0)
<<"\n";
std::cout<<
std::accumulate(v.begin(),v.end(),1,std::multiplies{})
<<"\n";
}
You can try it here.
In general, std::accumulate works on a range of any type, as long as the supplied operation,
is compatible with that type. While most of the time the operation passed to std::accumulate
is associative, it is important to know that it performs a left fold operation, which, if the binary operation
is not associative gives a different result than a right fold.
For example, the midpoint operation below is not associative. While the function foldr and foldl are
recursive, std::accumulate is not. It works similarly to my_accumulate.
#include <iostream>
#include <numeric>
#include <vector>
template<typename Iter, typename T, typename Func = std::plus<T> >
T my_accumulate(Iter start, Iter end, T init, Func f = std::plus<T>{}) {
T result = init;
for (auto itr = start; itr != end; ++itr) {
result =result+*itr;
}
return result;
}
template<typename T, typename ...Ts>
auto foldr(Ts... params) {
return (params + ... + T{});
}
template<typename T, typename ...Ts>
auto foldl(Ts... params) {
return (T{} + ... + params);
}
struct mid {
float _x;
mid(float x=0) :_x(x) {}
mid operator+(const mid& rhs) {
return mid((_x + rhs._x) / 2);
}
};
int main() {
std::vector<int> u{ 1,2,3,4 };
std::accumulate(u.begin(), u.end(), 0, std::plus{});
mid a{ 1 }, b{ 2 }, c{ 3 };
mid rr = foldr<mid>(a, b, c);
mid lr = foldl<mid>(a, b, c);
std::cout << rr._x << "\n";
std::cout << lr._x << "\n";
std::vector<mid> v{ a,b,c };
auto ar = std::accumulate(v.begin(), v.end(),mid{});
std::cout<<my_accumulate(v.begin(), v.end(), mid{})._x<<"\n";
std::cout << ar._x << "\n";
}
You can try the above code here.
Parallel accumulate
In this section we will modify the my_accumulate function to run its operations in parallel.
The basic idea is to divide the range into m subranges, where m is the number of threads we will run.
Each thread will accumulate the values in its own range, and when all the threads are done the main thread
will add the partial results.
Note that even though the parallel_acc function below applies
an arbitrary function f on the subranges, the final result is the sum of those partial results.
#include <iostream>
#include <thread>
#include <algorithm>
#include <vector>
#include <numeric>
#include "../include/utility.h"
using Long = unsigned long long;
/* assume the vector size is a power of 2 */
template <int NUMT=0,typename Iter,typename T,typename Func>
T parallel_acc(Iter first, Iter last, T init,Func f) {
Long const length = std::distance(first, last);
Long num_threads = NUMT==0?std::thread::hardware_concurrency():NUMT;
std::cout << "Number of threads = " << num_threads << "\n";
Long block_size = length / num_threads;
std::vector<T> results(num_threads ) ;
std::vector<std::thread> threads(num_threads );
Iter block_start, block_end;
for (Long i = 0; i < num_threads; ++i) {
block_start = first + i * block_size;
block_end = first+(i+1)*block_size;
threads[i] = std::thread(
[=](Iter s, Iter e, T& r) {
r = std::accumulate(s, e, 0.0,f);
},
block_start,block_end,std::ref(results[i])
);
}
for (auto& t : threads)
t.join();
return std::accumulate(results.begin(), results.end(), init);
}
int main()
{
const int n = 1<<25;
std::vector<double> v(n);
std::fill_n(v.begin(), n, 1.0);
Duration d;
double r;
TIMEIT(d
,r=parallel_acc<8>(v.begin(), v.end(), 0.0
, [](double acc, double val) {return acc += 1.0 / (1 + val * val); }
);
)
std::cout << "result= " << r << std::endl;
std::cout << "duration= " << d.count() << std::endl;
/* reference for std::accumulate
* https://tinyurl.com/yd9b4qz8
*/
TIMEIT(d
, r=std::accumulate(v.begin(), v.end(), 0.0
, [](double acc, double val) {return acc+=1.0 / (1 + val * val); }
);
)
std::cout << r << "\n";
std::cout << d.count() << "\n";
}
Example: Computing PI
In this section we will compute the value of PI both sequentially and in parallel. We will be using the below formula:
The basic idea, as in the previous example, is to divide the interval [0,1] into subintervals and compute each subinterval in a different thread than combine the results.
#include <iostream>
#include <thread>
#include <iomanip>
#include <mutex>
#include <vector>
#include "../include/utility.h"
void helper(double stepsize,int from,int to,double& res) {
double sum = 0, midpoint;
for (int i = from; i < to; ++i) {
midpoint = (i + 0.5) *stepsize;
sum += 1.0 / (1 + midpoint * midpoint);
}
std::lock_guard<std::mutex> g(m);
res += 4.0 *stepsize * sum;
}
template<int hard_t=2>
void par_pi(int pow, double& pi) {
const int num_steps = 1 << pow;
const int block_size = num_steps / hard_t;
std::vector<std::thread> mythreads;
double results[hard_t];
double dx = 1.0 / (double)num_steps;
pi = 0;
for (int t = 0; t < hard_t;++t) {
mythreads.push_back(
std::thread(
helper, dx, t * block_size, (t + 1) * block_size
,std::ref(results[t])
)
);
}
for (auto& t : mythreads)t.join();
pi = 0;
for (int i = 0; i < hard_t; ++i)
pi += results[i];
}
void seq_pi(int pow,double& pi) {
const int num_steps = 1 << pow;
helper(1.0 / num_steps, 0, num_steps, pi);
}
int main(){
double pi = 0;
Duration d;
TIMEIT(d
, par_pi<8>(28, pi);
)
std::cout <<std::setprecision(20) << pi << "\n";
std::cout << d.count() << "\n";
}
Computing sin(x)
In this section we compute the sine function for every element in an array. In addition to using multithreading, we will be using the Advanced Vector Extensions (AVX512) for x86 processors.
First we start with computing the sine for only one element x. To accomplish that we use the Taylor expansion
Clearly the value of sin(x) depends on the number of terms we compute in the Taylor expansion.
Computing sin for a single element
float seq_sin(int terms,float a){
float x=a;
float value=x;
float num=x*x*x;
float denom=6;
int sign=-1;
for(int j=1;i<=terms;++j){
value+=sign*num*denom;
num *=x*x;
denom *=(2*j+2)*(2*j+3);
sign *=-1;
}
return value;
}
In the above we have used the property that we can compute the numerator and denominator of a term based on its previous values as follows
- Since all the terms are odd so numerator=previous numerator * x *x
- The denominator contains the factorial of odd numbers so denominator=previous denominator* (2j+2)(2j+3). For example 5!=3! * 4 * 5 and j=2 so 5!=3! * (2j+2)(2j+3)
- The sign of a term is the negation of the previous term
Computing the sin for a range
We modify the previous code to handle the case where we want to compute the sin for a range of elements.
void seq_sin(int n,int terms, float* a, float* b) {
for (int i = 0; i < n; ++i) {
float x = a[i];
float value = x;
float num = x * x * x;
float denom = 6;
int sign = -1;
for (int j = 1; j <= terms; ++j) {
value += sign * num / denom;
num *= x * x;
denom *= (2 * j + 2) * (2 * j + 3);
sign *= -1;
}
b[i] = value;
}
}
Multi-threaded version
We can use multiple threads to compute the sin, or any function for that matter, for a range faster by subdividing the range between threads as we have done so far.
template<typename F>
void multit_sin(int terms, float* x, float* y,F f) {
int num_threads = std::thread::hardware_concurrency();
std::vector<std::thread> mythreads;
int block_size = n / num_threads;
for (int i = 0; i < num_threads; ++i) {
mythreads.push_back(
std::thread(f, block_size, terms, x, y)
);
x += block_size;
y += block_size;
}
for (int i = 0; i < num_threads; ++i)
mythreads[i].join();
}
USing AVX512
The Advanced Vector Extension (AVX) are extensions to the x86 instruction set which allow the CPU to perform a single instruction on multiple data (SIMD). In this section we use the AVX512 which allow us to compute a single instruction on 512 bits of data. For example, for a float which is typically 4 bytes, an AVX can compute the same operation on 16 floats at the same time. It is important to note that, in our case, we don’t expect a x16 speedup since there are other factors that come into play like memory transfers and cache invalidation.
#include <immintrin.h>
void vector_sin(int n,int terms, float* a, float* b)
{
for (int k = 0; k < LOAD; ++k) {
for (int i = 0; i < n; i += 16)
{
__m512 x = _mm512_load_ps(&a[i]);
__m512 value = x;
__m512 numer = _mm512_mul_ps(x, _mm512_mul_ps(x, x));//x^3
__m512 denom = _mm512_set1_ps(6);// 3 factorial
int sign = -1;
for (int j = 1; j <= terms; j++)
{
// value += sign * numer / denom
__m512 tmp = _mm512_div_ps(_mm512_mul_ps(_mm512_set1_ps(sign), numer), denom);
value = _mm512_add_ps(value, tmp);
numer = _mm512_mul_ps(numer, _mm512_mul_ps(x, x));
denom = _mm512_mul_ps(denom, _mm512_set1_ps((2 * j + 2) * (2 * j + 3)));
sign *= -1;
}
_mm512_store_ps(&b[i], value);
}
}
}
Combining both
Since the multi-threaded version can accept any function we can passed the AVX512 function. In fact this combination gives us the biggest speedup. Without going into too much details, since the computation is split over multiple cores, cache invalidation is minimized.