Parallel STL

Starting with C++17 most standard STL algorithms support parallel implementations. Most of those are algorithms can be used exactly like their sequential counterparts by including an execution policy. The execution policies that can be specified are (you need to include ):

std::execution::seq (sequential, default)
std::execution::par (parallel, multithreading)
std::execution::unseq (vectorized, C++20)
std::execution::par_unseq(parallel and vectorized)

As far as VC++2019 is concerned the implementation of ::par and ::par_unseq are the same. We will be using ::par and comparing it with the performance of ::seq.

Examples

Most algorithms in the STL have a parallel version (reference). In this exercise we will run a few of them and compare their performance with the sequential execution. To compile the code we need to make sure to set the c++17 for the compiler.

Visual C++ 2019: Project properties->General->C++ Language standard. Select C++17
MSVC: cl.exe /O2 /EHsc /nologo /std:c++17
Gnu C++ or Clang: c++ -O2 -std=c++17

#include <iostream>
#include <algorithm>
#include <numeric>
#include <vector>
#include <chrono>
#include <execution>
#include <random>
using Duration = std::chrono::duration<double, std::milli>;

#define TIMEIT(dur,...)\
   {\
    auto start = std::chrono::high_resolution_clock::now();\
    __VA_ARGS__\
    auto end = std::chrono::high_resolution_clock::now();\
     dur = std::chrono::duration<double, std::milli>(end - start);\
}

int main()
{
	const int n = 1 << 24;
	std::vector<double> u(n), v(n);
	Duration seq_d,par_d;
	std::fill(v.begin(), v.end(), 1.0);
	/* std::for_each */
	TIMEIT(seq_d,
		std::for_each( v.begin(), v.end(),
			[](double& x) {
				return  x /= 7.0;
			}
		);
	)
	TIMEIT(par_d,
		std::for_each(std::execution::par, v.begin(), v.end(),
			[](double& x) {
				return  x /= 7.0;
			}
		);
	)
	std::cout <<"for_each " <<seq_d.count()<<"\t"<<par_d.count() << "\n";
	/* std::transofrm */
	TIMEIT(seq_d,
		std::transform( v.begin(), v.end(), v.begin(),
			[](double& x) {
				return  x / 7.0;
			}
	);
	)
	TIMEIT(par_d,
			std::transform(std::execution::par, v.begin(), v.end(), v.begin(),
				[](double& x) {
					return  x / 7.0;
				}
			);
	)
	std::cout << "transform " << seq_d.count() << "\t" << par_d.count() << "\n";

	std::random_device rd;
	std::uniform_real_distribution<> dist(1, 10000);
	/* std::generate */
	TIMEIT(seq_d,
		std::generate(u.begin(), u.end(),
		[&]() {
			return dist(rd);
		}
	);
	)

	TIMEIT(par_d,
		std::generate(std::execution::par, v.begin(), v.end(),
		[&]() {
			return dist(rd);
		}
		);
	)
	std::cout << "generate " << seq_d.count() << "\t" << par_d.count() << "\n";
	/* reverse */

	TIMEIT(seq_d,
		std::reverse(u.begin(), u.end());
	)
		TIMEIT(par_d,
			std::reverse(std::execution::par, v.begin(), v.end());
	)
		std::cout << "reverse " << seq_d.count() << "\t" << par_d.count() << "\n";
	/* maximum */
	double seq_max, par_max;
	TIMEIT(seq_d,
		seq_max=*std::max_element(v.begin(), v.end());
	)
		TIMEIT(par_d,
		par_max=*std::max_element(std::execution::par, v.begin(), v.end());
	)
		std::cout << "max_element " << seq_d.count() << "\t" << par_d.count() << "\n";
	if (seq_max != par_max)std::cout << "error\n";

	/* std::sort  */

	TIMEIT(seq_d,
		std::sort(u.begin(), u.end());
	)
	TIMEIT(par_d,
		std::sort(std::execution::par,v.begin(), v.end());
	)
	std::cout << "sort " << seq_d.count() << "\t" << par_d.count() << "\n";
	/* std::count_if*/
	int seq_r,par_r;
	TIMEIT(seq_d,
		seq_r=std::count_if(u.begin(), u.end(),
			[](double x) {
				int i = x;
				return (i % 2 == 0);
			}
			);
	)
		TIMEIT(par_d,
			par_r=std::count_if(std::execution::par,u.begin(), u.end(),
				[](double x) {
					int i = x;
					return (i % 2 == 0);
				}
	);
	)
		std::cout << "count_if " << seq_d.count() << "\t" << par_d.count()<<"\n";
	if (seq_r != par_r)std::cout << "error\n";
}

OpenMP

OpenMP is a compiler extension for parallel programming. The code is annotated with preprocessor directives(pragma) to help the compiler parallelize the code. Below are the instructions to use OpenMP for common platforms

GNU g++: add the openmp switch, i.e. -fopenmp
Microsoft cl.exe: /openmp
Visual C++: Project Properties->C/C++->Language->OpenMP support (select yes)

In all platforms one should include the header omp.h.

Fork/Join Pattern

In our coverage of OpenMP, we will rely heavily on the fork/join pattern, or single program multiple data (SPMD), shown in the figure below.

fig

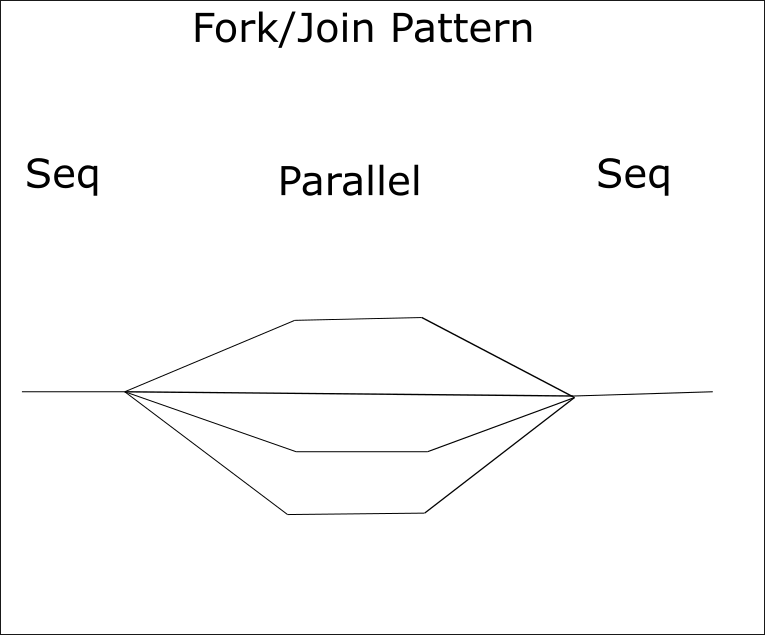
We have used this pattern extensively by explicitly creating and managing C++ threads. OpenMP will do most of that work for us.

The basic fork/join pattern is used in openMP as follows

#pragma omp parallel
{
    code to be run by all threads
}

The #pragma omp parallel will create a parallel region. This is equivalent to creating a number of threads at the beginning of the construct and joining them at the end. Obviously, to do useful work each thread should work on a different part of the data. To do so one should be able to tell which thread is running. This accomplished by the omp_get_thread_number() and omp_get_num_threads() calls.

We illustrate with the “hello world” of parallel programming, computing PI.

Computing PI

Recall that PI can be computed numerically using the expression below

$\pi=4\int_0^1\frac{dx}{1+x^2}$

We have done this computation before by explicitly creating C++ threads. In this example we let OpenMP do the bookkeeping for us.

int main()
{
	const int num_steps = 1 << 28;
	const double dx = 1.0 / (double)num_steps;
	const int num_threads = 8;
	omp_set_num_threads(num_threads);
	double results[num_threads]{};
	double d = omp_get_wtime();
#pragma omp parallel 
	{
		int nthreads = omp_get_num_threads();
		int block_size = num_steps / nthreads;
		int idx = omp_get_thread_num();
		double midpoint;
		for (int i = idx*block_size; i<(idx+1)*block_size ; ++i) {
			midpoint = (i + 0.5) * dx;
			results[idx] += 4.0 / (1 + midpoint * midpoint);
		}
	}

	double r = 0;
	for (int i = 0; i < num_threads; ++i)
		r += results[i];
	std::cout<<r*dx << "\n";
	d = omp_get_wtime() - d;
	/* duration in ms */
	std::cout << 1000 * d << "\n";
}

The first OpenMP call is omp_set_num_threads. This sets the maximum number of threads to be used. Next is the omp parallel directive creates the fork/join pattern. Notice that we use omp_get_num_threads() to get the actual number of threads being used. Usually this is the same value as num_threads but sometimes OpenMP cannot allocate the requested number of threads so it uses a smaller number but never larger. This is why when the array results is allocated we make sure it is initialized to 0 so that in the sum of all values at the end we are adding zeros if the actual number of threads is less than requested.

The next important call is omp_get_thread_num which returns the thread number and therefore allow us to specify on which region of the input the thread is acting on.

It is important to note that at the end of the omp parallel block, there is a hidden join, where the main thread waits for all other threads to finish.

The line results[idx]+=4/(1+midpoint*point) is a pattern that we have seen before many times. Each thread stores its partial result in a different location of the array and therefore there is no contention. Actually, this line of code results in poor performance due to repeated cache update. We have not seen this effect before because smart compilers (when optimization is used) usually optimize it away.

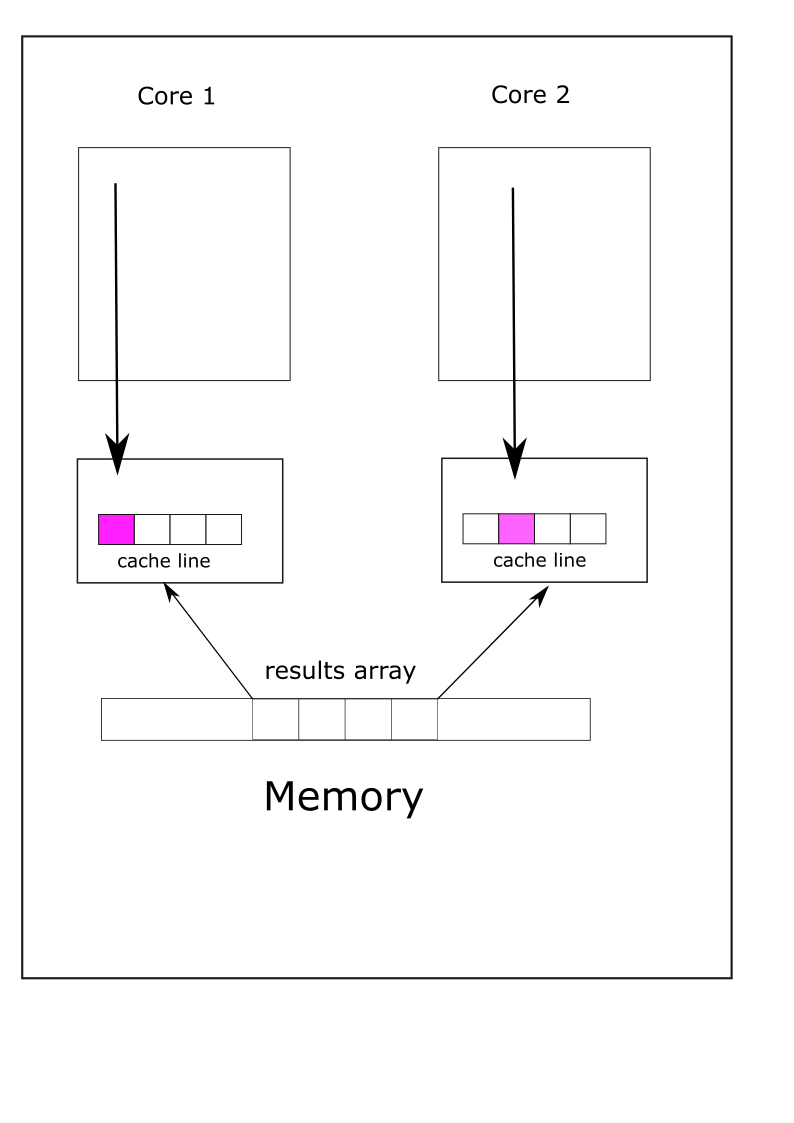
This problem is common enough that it was given a name: false sharing. The basic idea is that even though different threads are writing to different locations in the array but those locations are on the same cache line which forces cache invalidation/updates. We illustrate the situation in the figure below. Two threads on different cores, and thus using two different caches, access different locations of the results array. Even though there is no sharing of variables the array is small enough to fit in one cache line. When one thread updates a value in the array, all cores are notified that the corresponding cache line is invalidated and they reload the array from memory, creating unnecessary and very slow memory traffic.

We can eliminate this effect by using padding, i.e. keep enough distance between consecutive values of the results array so that each value is on a different cache line, which is typically 64 bytes for x86 and 128 bytes for ARM. Recall that C++ stores two dimensional arrays in row major mode. We can take advantage of that to store values on different cache lines as shown in the modified code below. fig

int main()
{
	const int num_steps = 1 << 28;
	const double dx = 1.0 / (double)num_steps;
	const int num_threads = 8;
	omp_set_num_threads(num_threads);
	alignas(64) double results[num_threads][8]{};
	double d = omp_get_wtime();
#pragma omp parallel 
	{
		int nthreads = omp_get_num_threads();
		int block_size = num_steps / nthreads;
		int idx = omp_get_thread_num();
		double midpoint;
		for (int i = idx*block_size; i<(idx+1)*block_size ; ++i) {
			midpoint = (i + 0.5) * dx;
			results[idx][0] += 4.0 / (1 + midpoint * midpoint);
		}
	}

	double r = 0;
	for (int i = 0; i < num_threads; ++i)
		r += results[i][0];
	std::cout<<r*dx << "\n";
	d = omp_get_wtime() - d;
	/* duration in ms */
	std::cout << 1000 * d << "\n";
}

cache line is 64 bytes so if the array is properly aligned the values in results accessed by each thread are on different cache lines.

Recommendation

Rather than padding with the added complexity of alignment it is easier and almost always preferable to use a variable local to the thread in the loop. At the end set the results to that variable.

		for (int i = idx*block_size; i<(idx+1)*block_size ; ++i) {
			midpoint = (i + 0.5) * dx;
			r+= 4.0 / (1 + midpoint * midpoint);
		}
		results[idx] = r;

Exercise

The above behavior is usually masked if we use optimization. To observe it we need to compile without optimization. In the repository cd to the false_sharing folder and use the following compilation commands:

On Windows open a developer power shell and type

  cl.exe /openmp /nologo /EHsc /DX file_sharing.cpp

On Unix/Linux with GNU C++:

 c++ -fopenmp -DX file_sharing.cpp

Where X can take three different values:

FALSE_SHARING: this case illustrates false sharing. Its running time is approximately 4-5 times slower.
ALIGN: this case uses a 2-d array were each “row” is aligned on a different cache line. This is 4-5 times faster than the previous case.
LOCAL: this case uses a local variable it has the same running time as the previous case.

Parallel for

Apart from creating and managing the threads the parallel construct is similar to what we have done with C++ threads. We need to keep track of the thread id and manually divide the work among the threads. OpenMP can help automate the work distribution by using the parallel for construct.

Immediately prior to the use of the for loop we add the directive #pragma omp for.

#pragma omp parallel 
	{
#pragma omp for reduction(+:sum)
pragma omp for
			for (int i = 0; i <num_steps; ++i) {
				midpoint = (i + 0.5) * dx;
				sum += 1.0 / (1 + midpoint * midpoint);
			}
	}

The clause reduction(+:sum). OpenMP will create a private copy of the variable sum initialized to zero (the identify of +). After the loop the private copies are added to produce the final value. In openmp creates local copies of the index i. There is an implicit barrier at the end of the loop construct.

Nested loops

The OpenMP for construct automatically makes the index of the loop immediately after the construct private. This does not apply to subsequent loops. In the example below, i is automatically privatized whereas j and tmp are not so we have to declare them private.

#pragma omp parallel
{
#pragma omp for private(j,tmp)
   for(int i=0;i<n;++i){
	   for(int j=0;j<n;++j)
	    tmp=do_something(i,i)
   }
}

Schedule

The for construct automatically divides the range into subranges (called chunks in OpenMP), and each thread works on a chunk. This is fine as long as the work needed on each chunk has more or less the same cost. Sometimes the work is uneven which gives some threads much more work than others. Consider the following example

void sleepFor(int n) {
   
#pragma omp parallel 
    {
#pragma omp for 
        for (int j = 1; j <=     n; ++j) {
            std::this_thread::sleep_for(std::chrono::seconds(j));
        }
    }
}

Assume that the total number of threads is set to 4 and we call sleepFor(16). Then OpenMP will divide the loop on the threads as follows

Thread 1 will process 1,2,3,4 for a total of 10s
Thread 2 will process 5,6,7,8 for a total of 26s
Thread 3 will process 9,10,11,12 for a total of 42s
Thread 4 will process 13,14,15,16 for a total of 58s

Therefore the completion time is 58s. It is clear from the above that the first two threads will be idle for a long time. OpenMP allow us to change the assignment of chunks to threads using the schedule clause. While there are different schedules we will cover the dyanmic type here.

void sleepFor(int n) {
   
#pragma omp parallel 
    {
#pragma omp for schedule(dynamic)
        for (int j = 1; j <=     n; ++j) {
            std::this_thread::sleep_for(std::chrono::seconds(j));
        }
    }
}

In this case OpenMP maintains a chunk queue and whenever a thread finishes the chunk it is working on it will be assigned the next available one. Repeating the above example with dynamic schedule will assign the threads as follows

Thread 1 will process 1,5,9,13 for a total of 28s
Thread 2 will process 2,6,10,14 for a total of 32s
Thread 3 will process 3,7,11,15 for a total of 36s
Thread 4 will process 4,8,12,16 for a total of 40s

Therefore the completion time is 40s instead of 58s using the default schedule. Also, one can specify the chunk size, i.e. schedule(dynamic,chunk) with a default of 1.

OpenMP tasks

The looping-contructs we have convered so far are good for regular programs. Irregular and recursive are hard to program in that. For such programs we use tasks introduced in OpenMP 3.0. Tasks are independent units of work instead of thread. basic syntax

#pragma omp task

// quicksort.cpp : This file contains the 'main' function. Program execution begins and ends there.
//

#include <iostream>
#include <vector>
#include <random>
#include <algorithm>
#include <omp.h>
const int n = 1 << 24;
const int cutoff = 1 << 18;
template <typename Iter>
Iter partition(Iter start, Iter end) {
	/* assume the input is random and select the
	* first element as pivot
	*/
	double pivot_value = *start;
	auto i = start, j = end - 1;
	while (i != j) {
		while (i != j && pivot_value < *j) --j;
		while (i != j && *i <= pivot_value) ++i;
		std::iter_swap(i, j);
	}
	std::iter_swap(start, i);
	return i;
}

template<typename Iter>
void seqQuicksort(Iter start, Iter end) {
	{
			auto d = std::distance(start, end);
			if (d <= cutoff) {
				std::sort(start, end);
			}
			else {
				Iter mid = partition(start, end);
#pragma omp task
				seqQuicksort(mid + 1, end);
#pragma omp task
				seqQuicksort(start, mid);
			}
		
	}
}
int main()
{	
	std::vector<float> v(n);
	std::random_device rd;
	std::uniform_real_distribution<float> dist(1, 100);
	std::generate(v.begin(), v.end(),
		[&]() {
			return dist(rd);
		}
		);
	std::cout << "omp start\n";
	double d = omp_get_wtime();
#pragma omp parallel
	{
#pragma omp single
		seqQuicksort(v.begin(), v.end());
	}
	d = omp_get_wtime() - d;

	std::cout <<"is sorted="<< std::is_sorted(v.begin(), v.end());
	std::cout << "\n" << 1000*d << "\n";
}

Since the omp parallel construct creates a team of threats it is essential for the first call to seqQuicksort be performed by only one of them hence the omp single construct.

Note on compilers

The MSVC compiler lags in OpenMP support. The task construct can be enabled by passing the following switches to cl.exe

-opemmp:llvm -openmp:experimental

even though it compiles with the above switches MSVC on my computer crashes. So you are better off using clang++. Start you Visual Studio installer, under the workloads choose Desktop development for C++ and in the details choose C++ lang tools for windows.

Previous submodule:

Concurrency2

Next submodule:

Cuda1